定義與作用:
單因素方差分析用於1個定類欄位(X)與 1 個或 1 個以上的定量欄位(Y)之間的差異性研究。單因素方差分析測試某一個控制變數的不同水準是否給觀察變數造成了顯著差異和變動。例如,培訓是否給學生成績造成了顯著影響;不同地區的考生成績是否有顯著的差異等。
基本假設:
在單因素實驗中,記因素為A,設其中有k個水準,記為A1,A2,…,Ak,在每個水準下考察的指標可以看成一個總體,則現有k個總體,在方差分析時需要滿足以下假定:
- 每個總體都服從正態分佈;
- 各總體滿足方差齊性;
- 每個總體抽取的樣本都是相互獨立的,不存在多重線性相關。
分析步驟:
- 提出假設
原假設H0 : a1 = a2 = …… = ak 、備擇假設H1 : a1、a2、……、ak不全相等。若原假設H0成立,則因素A的不同水準對指標的影響是無顯著差異的,若原假設H0不成立,則因素A的不同水準對指標的影響是有顯著差異。
2. 構造檢驗統計量
首先對因素 A 不同水準下的均值進行計算:
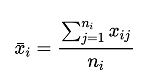
i = 1,2,…k ,其中,ni 是第 i 個總體實驗資料的個數;然後通過所有水準的均值確定計算全部觀測值的總均值:
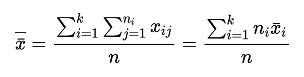
再者就是計算 3 個誤差平方和構造檢驗統計量———總誤差平方和、因素誤差平方(組間平方和)以及隨機誤差平方和(組內平方和),分別是 SST、SSA、SSE,其計算公式如下:

為了保證誤差平方和計算的準確性可以利用各平方和計算的結果除以各自對應的自由度轉變為均方進行度量,依次對應的自由度為 n-1、k-1、n-k。
SSA 的均方也被稱為組間均方或組間方差,記為 MSA 。計算公式可以表示為MSA = 組間平方和/自由度 = SSA / (k – 1);
SSE 的均方也被稱為組內均方或組內方差,記為 MSE 。其計算公式為: MSE = 組內平方和/自由度 = SSE/( n – k) 。
通過MSA、MSE的比值即可以得到所需的 F 檢驗統計量,如下圖所示:
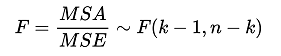
3. 確定臨界值
根據給定的顯著性水準α、分子(組間均方)自由度 df1 = k – 1 、分母(組內均方)自由度 df2 = n – k ,查找Fα(k – 1,n – k),確定相應的臨界值。
4. 作出決策
將步驟2得到的F值與步驟3中的 α 水準臨界值Fα(k – 1,n – k)進行比較,做出決策。若 F > Fα ,則拒絕原假設,即 H0 : a1 = a2 =…= ak 的假設不成立,表明因素A的不同水準對指標的影響是有顯著差異的;F < Fα,則不能拒絕原假設H0,因素A的不同水準對指標的影響是無顯著差異的。在進行統計決策時,還可以直接利用方差分析表中輸出 P 值與顯著性水準 α 進行比較,得出結論。
參考文獻:
- 牛凯.数据分析之单因素方差分析[J].产业与科技论坛,2019(2):57-58.
- 田霞,徐瑞民编. 概率论与数理统计 人工智能专用. 北京:中国纺织出版社, 2021.05.
- Kim T K. Understanding one-way ANOVA using conceptual figures[J]. Korean journal of anesthesiology, 2017, 70(1): 22-26.
