一、概要

線性迴歸用於確定兩種或兩種以上變數間相互依賴的定量關係，只有一個自變數的情況稱為單元線性迴歸，大於一個自變數的情況稱為多元線性迴歸。線性迴歸通常用於預測分析，廣泛應用在經濟、醫學和工業等領域。

二、詳細介紹

（一）模型介紹

1.迴歸分析方法

(1)統計學上，用一個函數關係式將依變數隨自變數變化而變化的關係呈現出來，並稱其為迴歸方程式(對樣本而言)或迴歸模型(對總體而言) 。迴歸分析通常包括構建迴歸方程式、對其迴歸係數進行假設檢驗和區間估計(即由樣本去推論總體的規律，在本質上是希望得到或接近迴歸模型) ，最終目的是在給定自變數的值的條件下，預測依變數的值; 少數情境下，會給定依變數的值，把握自變數的值區間(即用於控制) 。

(2)迴歸分析按涉及自變數的多少，分為單元迴歸和多元迴歸。按照依變數的類型，可分為線性迴歸分析和非線性迴歸分析。

2.公式

依變數（Y）和一個或多個自變數（X）之間建立的一種迴歸方程式。

一元迴歸：

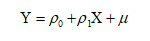
多元迴歸：

3. 指標說明

R平方： 判定係數，用於衡量迴歸模型對樣本觀察值的配適度，數值範圍為0-1，值越接近1，模型的配適度越高。

調整後R平方：修正自由度的判定係數，用於衡量迴歸模型對樣本觀測值的配適度，數值範圍為0-1，數值越接近1，模型的配適度越高。

F：F值用於判定模型中依變數與所有自變數之間的線性關係在總體上是否顯著。

AIC：AIC是權衡估計模型的複雜度和模型擬合資料優良性的標準，用於模型選擇，通常選擇AIC最小的模型。

BIC：貝氏訊息準則與AIC相似，用於模型選擇。

B: 模型的迴歸係數，包括截距和斜率顯著性小於0.05時有意義。

標準誤差：迴歸係數標準誤差，值越大表示迴歸係數的估計值越不可靠。

t：對自變數進行顯著性檢定，以確定變數是否被保留在模型中。

Sig：顯著性，如果0.01<sig<0.05，為差異顯著，如果sig<0.01，則為差異極顯著。

（二）研發依據

 [1] Robinson, E. (2016). Introduction to Likelihood Statistics. Retrieved April 16, 2021 from: https://hea-www.harvard.edu/AstroStat/aas227_2016/lecture1_Robinson.pdf

[2] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.