K-Means 演算法是一種無監督學習，同時也是基於劃分的聚類演算法，一般用歐式距離作為衡量資料物件間相似度的指標，相似度與資料物件間的距離成反比，相似度越大，距離越小。演算法需要預先指定初始聚類數目 k 以及 k 個初始聚類中心，根據資料物件與聚類中心之間的相似度，不斷更新聚類中心的位置，不斷降低類簇的誤差平方和（Sum of Squared Error，SSE），當 SSE 不再變化或目標函數收斂時，聚類結束，得到最終結果。

核心思想是首先從資料集中隨機選取 k個初始聚類中心C_i(1 ≤ i ≤ k)，計算其餘資料物件與聚類中心Ci的歐氏距離，找出離目標資料物件最近的聚類中心C_i，並將資料物件分配到聚類中心C_i所對應的簇中。然後計算每個簇中資料物件的平均值作為新的聚類中心，進行下一次反覆運算，直到聚類中心不再變化或達到最大的反覆運算次數停止。

空間中資料物件與聚類中心間的歐式距離計算公式為：

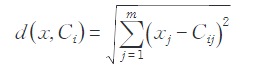
其中，x為資料物件，C_i為第 i個聚類中心，m為資料物件的維度，x_j，C_ij 為x和 C_i的第j個屬性值。
整個資料集的誤差平方和 SSE 計算公式為：

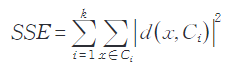
本分析方法中，如果涉及定類變數聚類，則會先對定類變數進行編碼，然後再進行聚類。假如輸入的變數存在缺失值，定類資料自動以眾數填補，定量資料自動以平均數填補。

參考文獻：

• 杨俊闯,赵超.K-Means聚类算法研究综述[J].计算机工程与应用,2019,55(23):7-1463
• Yadav J, Sharma M. A Review of K-mean Algorithm[J]. Int. J. Eng. Trends Technol, 2013, 4(7): 2972-2976.