一、Summary
Binary logistic regression is a linear model for binary classification predictive modeling. As a powerful data analysis technique wherein we seek to understand how different random quantities relate to one another, it is widely used in Sociology, Biostatistics, Clinics, Quantitative psychology, and Econometrics.
二、Detailed introduction
(一)Model introduction
- Logistic regression method
(1) Logistic regression is a statistical model that in its basic form uses a logistic function to model a binary dependent variable, although many more complex extensions exist. As a kind of generalized linear regression, it has many similarities with multiple linear regression analysis. The model form is basically the same, the difference is that the dependent variable is different, multiple linear regression directly uses wx+b as the dependent variable, while logistic regression uses the function L to correspond wx+b to a hidden state p, that is, p=L(wx+b ), and then determine the value of the dependent variable according to the size of p and 1-p. If L is a logistic function, it is logistic regression, and if L is a polynomial function, it is polynomial regression.
(2) The dependent variable of logistic regression can be binary or multi-category, but binary is more commonly used and easier to interpret. Multi-category can be processed using the softmax method. The most commonly used in practice is the binary logistic regression.
2. Formula
A regression equation established between the dependent variable (Y) and one or more variables (X).
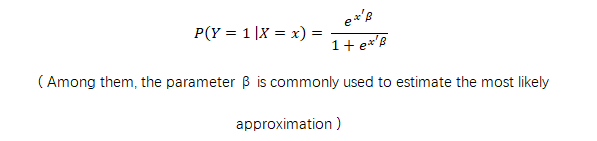
3. Index description
-2log likelihood: The -2 times of the natural logarithm of the value of the likelihood function reflects the model’s fitness. The smaller the value, the more fit of the model.
Pseudo R-squared:McFadden’s pseudo-R squared, a measure used to measure how the regression model fits the observed value of the sample. The value range is 0-1. The closer the value is to 1, the more fit of the model.
AIC:The Akaike information criterion (AIC) is a mathematical method for evaluating how well a model fits the data it was generated from. The best-fit model according to AIC is the one that explains the greatest amount of variation using the fewest possible independent variables.
BIC:Bayesian Information Criterion is similar to AIC for model selection.
B:The regression model is significant when the coefficient (including intercept and slope significance) is less than the usual significance level of 0.05. The slope indicates the steepness of a line and the intercept indicates the location where it intersects an axis.
Standard error:The greater the standard error of the regression coefficient, the less reliable the estimated value of the regression coefficient.
z: Conduct a significance test on the independent variables to determine whether the variables will be retained in the model.
Sig:Significance, if 0.01<sig<0.05, the difference is significant, and if sig<0.01, the difference is extremely significant.
Exp(B): Odds ratio
(二)References
[1] Edge, M. (2021). Statistical Thinking from Scratch: A Primer for Scientists.
[2] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
