Introduction:
The K-Means clustering (numeric) is a type of unsupervised learning, and it is also a clustering algorithm based on division. Generally, Euclidean distance is used as an index to measure the similarity between data objects. The similarity is inversely proportional to the distance between data objects, meaning the greater the similarity, the smaller the distance. The greater the similarity, the greater the similarity. The smaller the distance. The algorithm requires specifying the initial number of clusters k and k initial cluster centers in advance, and continuously update the position of the cluster centers according to the similarity between the data objects and the cluster centers, and continuously reduce the sum of squared errors (Sum of Squared) of the clusters. Error, SSE). When the SSE no longer changes or the objective function converges, the clustering ends, and the final result is obtained.
Main idea:
First, randomly select k initial cluster centers Ci (1 ≤ i ≤ k) from the data set, calculate the Euclidean distance between the remaining data objects and the cluster centers Ci, find out the cluster center Ci closest to the target data object, and assign the data objects to the clusters corresponding to the cluster centers Ci. Then calculate the average value of the data objects in each cluster as the new cluster center, and proceed to the next iteration until the cluster center no longer changes or until the maximum number of iterations is reached to stop.
The formula for calculating the Euclidean distance between the data object and the cluster center in the space is:
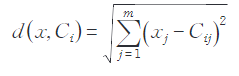
Among them, x is the data object, Ci is the ith cluster center, m is the dimension of the data object, xj, Cij are the jth attribute values of x and Ci.The sum of squared errors (SSE) for the entire dataset is calculated as:
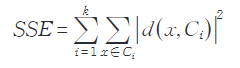
Among them, the size of SSE indicates the quality of clustering results, and k is the number of clusters.
In this analysis method, if clustering of definite variables is involved, the definite variables will be coded first, and then clustered. If there are missing values in the input variables, the categorical data are automatically filled with the mode, and the quantitative data are automatically filled with the mean.
References:
- Yadav, J., & Sharma, M. (2013). A Review of K-mean Algorithm. Int. J. Eng. Trends Technol, 4(7), 2972-2976.
- Li, Y., & Wu, H. (2012). A clustering method based on K-means algorithm. Physics Procedia, 25, 1104-1109.
- Ahmed, M., Seraj, R., & Islam, S. M. S. (2020). The k-means algorithm: A comprehensive survey and performance evaluation. Electronics, 9(8), 1295.
