DiVoMiner® User Manual

  2. Home
  4. Docs
  6. DiVoMiner® User Manual
  8. Advanced statistics
  10. t-Test

t-Test

1. t-Test

The t test, also known as the student’s t-test, is a statistical hypothesis test used to determine whether there is a significant difference between the means of two independent samples. It is often used in research and data analysis to test hypotheses about the mean of a small sample drawn from a normally distributed population when the population standard deviation is unknown. The t-test uses the t-distribution theory to infer the probability of a difference, and compares whether the difference between two means is significant. Here are the differences between some of the most common tests of hypothesis:

2. One-sample, two-sample, and paired t test

There are different types of t test based on whether the groups being compared come from a single population or two different populations: one-sample, two-sample (a.k.a the independent t-test), the paired t-test. If there is one group being compared against a standard value, perform a one-sample t test; the independent samples t-test compares the means of two separate groups, and the paired t-test compares the means of two related groups.

The one-sample t-test is used to analyze whether the quantitative data (in a normal distribution) is significantly different from a given value, such as comparing the acidity of a liquid to a neutral pH of 7. The formula for the one-sample t-test is:

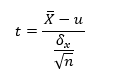
Where   is the mean of the sample, μ is the overall mean, is the standard deviation of the sample, and n is the sample size. The statistic t obeys the t-distribution with n degrees of freedom under the condition that the null hypothesis: μ=μ0 is true.

The two-sample (independent sample) t-test is used to test the differences in two different populations, such as to test whether there is a significant difference in two different species, or people from two separate cities. The formula for the independent samples t-test is:

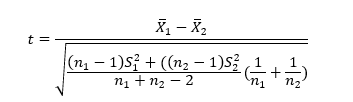
Among them, and  are the two-sample variance, and  and  are the two-sample capacity.

The paired sample t-test is a within-subjects design often used in experimental research, to test the differences in the data obtained by two groups of data obtained under different conditions. For example, compare whether there is a significant difference in the purchase intention of the sample in the context of advertisements and no advertisements. The formula for the paired t-test is:

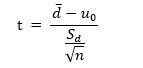
where dbar = mean difference, sd/√n = standard error = standard deviation of the difference / sqrt of number of samples.

3. One-tailed or two-tailed t test

Based on whether you want to test the difference in a specific direction, there is one-tailed t-test and two-tailed t-test. A one-tailed t-test, also known as a directional t-test, is a statistical hypothesis test where the null hypothesis specifies that the mean of the population is either greater than or less than a certain value. Thus, the alternative hypothesis is that the mean is in the opposite direction. One-tailed t-tests are used when the researcher has a clear directional hypothesis or when it is only important to detect differences in one direction. A two-tailed t-test, also known as a non-directional t-test, is a statistical hypothesis test where the null hypothesis specifies that the mean of the population is equal to a certain value. The alternative hypothesis is that the mean is either greater than or less than the null hypothesis value. Two-tailed t-tests are used when the researcher does not have a clear directional hypothesis or when it is important to detect differences in both directions. In practice, the choice of an appropriate t test depends on the research question, the available data, and the hypotheses being tested.

4. Perform t-Test on DiVoMiner®

On DiVoMiner® platform, click “Statistical analysis – Advanced statistics – Create a calculation task – t-Test”. More statistical tests will be released soon. Stay tuned!

5. References:

Was this article helpful? Yes No

How can we help?